前言:
以前写PHP一个MD5验证小程序(脑残基别)的时候遇到了一个问题,我处理后的MD5与其他网站在线转化的值不相同,后来知道我用了str_replace函数处理,即使字符串没有发生改变,但是MD5值已经发生了巨大的变化!很神奇吧,MD5加密被用于几乎所有验证类型程序中去。
但是,据说2004年山东大学的王小云教授破解了MD5,写出了逆算方法!!世界强大的MD5大厦轰然倒塌,连美国都好怕怕,紧急更换了加密方式。中国好牛逼的说~~MD5已经不安全了!这是真的么?
在2004年8月,国际密码学界对王小云这个名字并不熟悉。2004年8月,在美国加州圣芭芭拉召开的国际密码大会上,并没有被安排发言的王小云教授拿着自己的研究成果找到会议主席,会议主席破例给了她15分钟时间来介绍自己的成果,而通常发言人只被允许有两三分钟的时间。王小云与助手展示了MD5、SHA-0及其他相关杂凑函数的杂凑冲撞。所谓杂凑冲撞指两个完全不同的讯息经杂凑函数计算得出完全相同的杂凑值。根据鸽巢原理,以有长度限制的杂凑函数计算没有长度限制的讯息是必然会有冲撞情况出现的。可是,一直以来,电脑保安专家都认为要任意制造出冲撞需时太长,在实际情况上不可能发生,而王小云等的发现可能会打破这个必然性。就这样,王小云在国际会议上首次宣布了她及她的研究小组的研究成果——对MD4、MD5、HAVAL-128和RIPEMD等四个著名密码算法的破译结果。
事实:
什么是MD5:
事实上,md5不属于加密算法,它属于单项散列算法的一种,也就是摘要算法。它经过复杂的运算,将文件提取成为一个固定长度的DNA(信息)只专属于这个文件,一旦文件发生微小的改动,DNA就会发生变化,即使你经过删除字节,添加字节的处理,也会发生变化。
山东大学教授王小云“破解”了MD5?
事实上,MD5不可能进行逆运算。很多人很为之骄傲的山东大学王小云教授的关于什么MD5″解密”的新闻。我只能说那些报道这则消息的新闻工作者的无知!(当然不能怪他们,因为他们不是计算机专业毕业的,而且报道的又是有关计算机安全学方面的东西。)
王小云被报道的所谓“解密”其实不是写出了什么逆算法,而是“碰撞”。MD5碰撞法。你可能不知道这是什么,我给你解释下,比如字符串 “12223dsfd说sads2323啊啊”经过计算得到MD5值,而字符串“……”经过计算也是得到固定长度的MD5值,也就是说无数个字符串进行散列加密后都是得到固定长度的MD5值,呢么MD5 最长32位的加密值以数字+字母的形式组合,大概有N种结果。不过你忘了,字符串不限长度的组合运算,一定存在MD5值1对多的这种情况。这就是MD5碰撞法的内容核心,虽然这种概率极低,但是如果你非要找的话它一定存在。MD5——密文与明文事实上并不是单一对应。
MD5作为散列算法,一般用于验证。打个比方假如password=“123”,经过MD5运算后值为“202CB962AC59075B964B07152D234B70”而作为字符串的排列一定存在password=“XXXX………………”的值也是“202CB962AC59075B964B07152D234B70”那么这时候我们就可以输入“XXXX………………”来进行登录。 这就叫做碰撞破解。
这貌似在家里睡觉也能想到这种情况,它一定存在。注意“破解”不是指的逆算方法,而是利用MD5的漏洞欺骗。像网上那种输入密文转换明文用的是数据库,也就是已有的验证(人工提交)的明文和密文。对于复杂的密码,数据库里是没有的,因为没人能够逆算出来。
MD5还安全么?
ps:这种碰撞的几率….王小云只是证明他存在,甭管字符串或者文件经过怎么样的修改来进行欺骗。比如说“123”的MD5值,可能需要字符几亿来欺骗对撞。即散列算法使用来验证,哪个验证者会不计数据长度来让你验证,在程序与数据库中已经限定了varchar长度或者int长度。况且对撞的可能性几乎为0,在数学是是不确定事件(刚去问俺爹)。这个不确定事件可以定义为不可能事件。这种概率跟在全世界沙漠里,找到两个构成完全一样的沙子一样困难。
王小云教授的贡献在于她找到了一种方法,可以在已知原文的情况下构造出另一个跟原文MD5值相同的串。并且该计算过程所消耗的时间是有限的、可计算的。不过,要利用此方法达成某种目的依然是困难无比的,原因就是你无法确定新构造出来的串符合你的预期。 也就是我上面举的例子。
再举个例子,我现在有一个MD5密文,根据MD5碰撞原理,我这个密文对应了N个MD5明文,我们可以限定长度得到明文进行登录,可是不要忘了,你这就属于猜解的范畴了,不属于逆算,而且时间是不可控的,这个角度我们可以直接获得正确的明文。但是对于软件和验证来说已经超越了预期,即使你得到了,也是毫无功能的充满奇怪字符组合的文件。
我可以说MD5现在还安全,只要你不使用库里存在的密码组合。ps:1234,admin 之类的。MD5根本不存在逆算法,王小云也算不上破解,因为这不是一个逆向还原的过程。MD5对撞仍然是个想法,需要进行大量逻辑运算,算到猴年马月也不一定,对于这种通过MD5正算方法计算再进行密文比对的方式来说,你的计算器首先要实现高速度的计算MD5值,而对于长度及其长的欺骗(对撞法)来说,随着明文长度的增加,计算时间也成比增长。
后记:
MD5妥妥的,安全得很,说MD5不安全只是捕风捉影。MD5的运算原理到底是什么呢?我在文章末尾给出,能写出逆算法的联系我…..
第二步、记录信息长度:用64位来存储填充前信息长度。这64位加在第一步结果的后面,这样信息长度就变为N*512+448+64=(N+1)*512位。
第三步、装入标准的幻数(四个整数):标准的幻数(物理顺序)是(A=(01234567)16,B=(89ABCDEF)16,C=(FEDCBA98)16,D=(76543210)16)。如果在程序中定义应该是(A=0X67452301L,B=0XEFCDAB89L,C=0X98BADCFEL,D=0X10325476L)。有点晕哈,其实想一想就明白了。
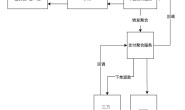
第四步、四轮循环运算:循环的次数是分组的个数(N+1)
1)将每一512字节细分成16个小组,每个小组64位(8个字节)
2)先认识四个线性函数(&是与,|是或,~是非,^是异或)
G(X,Y,Z)=(X&Z)|(Y&(~Z))
H(X,Y,Z)=X^Y^Z
I(X,Y,Z)=Y^(X|(~Z))
3)设Mj表示消息的第j个子分组(从0到15),<<<s表示循环左移s位,则四种操作为:
GG(a,b,c,d,Mj,s,ti)表示a=b+((a+G(b,c,d)+Mj+ti)<<<s)
HH(a,b,c,d,Mj,s,ti)表示a=b+((a+H(b,c,d)+Mj+ti)<<<s)
II(a,b,c,d,Mj,s,ti)表示a=b+((a+I(b,c,d)+Mj+ti)<<<s)
4)四轮运算
a=FF(a,b,c,d,M0,7,0xd76aa478)
b=FF(d,a,b,c,M1,12,0xe8c7b756)
c=FF(c,d,a,b,M2,17,0x242070db)
d=FF(b,c,d,a,M3,22,0xc1bdceee)
a=FF(a,b,c,d,M4,7,0xf57c0faf)
b=FF(d,a,b,c,M5,12,0x4787c62a)
c=FF(c,d,a,b,M6,17,0xa8304613)
d=FF(b,c,d,a,M7,22,0xfd469501)
a=FF(a,b,c,d,M8,7,0x698098d8)
b=FF(d,a,b,c,M9,12,0x8b44f7af)
c=FF(c,d,a,b,M10,17,0xffff5bb1)
d=FF(b,c,d,a,M11,22,0x895cd7be)
a=FF(a,b,c,d,M12,7,0x6b901122)
b=FF(d,a,b,c,M13,12,0xfd987193)
c=FF(c,d,a,b,M14,17,0xa679438e)
d=FF(b,c,d,a,M15,22,0x49b40821)第二轮
a=GG(a,b,c,d,M1,5,0xf61e2562)
b=GG(d,a,b,c,M6,9,0xc040b340)
c=GG(c,d,a,b,M11,14,0x265e5a51)
d=GG(b,c,d,a,M0,20,0xe9b6c7aa)
a=GG(a,b,c,d,M5,5,0xd62f105d)
b=GG(d,a,b,c,M10,9,0×02441453)
c=GG(c,d,a,b,M15,14,0xd8a1e681)
d=GG(b,c,d,a,M4,20,0xe7d3fbc8)
a=GG(a,b,c,d,M9,5,0x21e1cde6)
b=GG(d,a,b,c,M14,9,0xc33707d6)
c=GG(c,d,a,b,M3,14,0xf4d50d87)
d=GG(b,c,d,a,M8,20,0x455a14ed)
a=GG(a,b,c,d,M13,5,0xa9e3e905)
b=GG(d,a,b,c,M2,9,0xfcefa3f8)
c=GG(c,d,a,b,M7,14,0x676f02d9)
d=GG(b,c,d,a,M12,20,0x8d2a4c8a)
第三轮
a=HH(a,b,c,d,M5,4,0xfffa3942)
b=HH(d,a,b,c,M8,11,0x8771f681)
c=HH(c,d,a,b,M11,16,0x6d9d6122)
d=HH(b,c,d,a,M14,23,0xfde5380c)
a=HH(a,b,c,d,M1,4,0xa4beea44)
b=HH(d,a,b,c,M4,11,0x4bdecfa9)
c=HH(c,d,a,b,M7,16,0xf6bb4b60)
d=HH(b,c,d,a,M10,23,0xbebfbc70)
a=HH(a,b,c,d,M13,4,0x289b7ec6)
b=HH(d,a,b,c,M0,11,0xeaa127fa)
c=HH(c,d,a,b,M3,16,0xd4ef3085)
d=HH(b,c,d,a,M6,23,0x04881d05)
a=HH(a,b,c,d,M9,4,0xd9d4d039)
b=HH(d,a,b,c,M12,11,0xe6db99e5)
c=HH(c,d,a,b,M15,16,0x1fa27cf8)
d=HH(b,c,d,a,M2,23,0xc4ac5665)
第四轮
a=II(a,b,c,d,M0,6,0xf4292244)
b=II(d,a,b,c,M7,10,0x432aff97)
c=II(c,d,a,b,M14,15,0xab9423a7)
d=II(b,c,d,a,M5,21,0xfc93a039)
a=II(a,b,c,d,M12,6,0x655b59c3)
b=II(d,a,b,c,M3,10,0x8f0ccc92)
c=II(c,d,a,b,M10,15,0xffeff47d)
d=II(b,c,d,a,M1,21,0x85845dd1)
a=II(a,b,c,d,M8,6,0x6fa87e4f)
b=II(d,a,b,c,M15,10,0xfe2ce6e0)
c=II(c,d,a,b,M6,15,0xa3014314)
d=II(b,c,d,a,M13,21,0x4e0811a1)
a=II(a,b,c,d,M4,6,0xf7537e82)
b=II(d,a,b,c,M11,10,0xbd3af235)
c=II(c,d,a,b,M2,15,0x2ad7d2bb)
d=II(b,c,d,a,M9,21,0xeb86d391)
5)每轮循环后,将A,B,C,D分别加上a,b,c,d,然后进入下一循环。